

Next: Convolution filter
Up: Mathematical Derivations
Previous: Discretizing the Navier-Stokes-Equation
Substituting
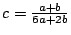 ,
,
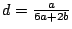 ,
,
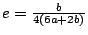 we obtain:
we obtain:
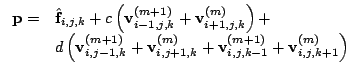 |
(19) |
Setting
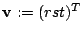 we may write
we may write
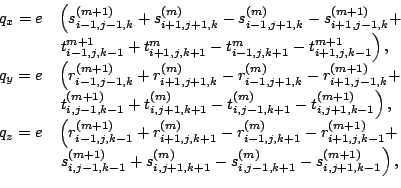 |
(20) |
hence for the residual vector
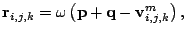 |
(21) |
and the SOR update of
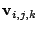 is given by
is given by
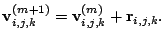 |
(22) |
Gert Wollny
2003-03-17
![]() ,
,
![]() ,
,
![]() we obtain:
we obtain:
![]() we may write
we may write