

Next: SOR update
Up: Mathematical Derivations
Previous: Mathematical Derivations
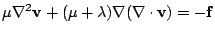 |
(12) |
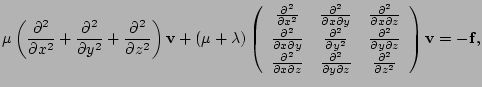 |
(13) |
For the x-component of (13) we may write:
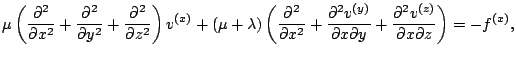 |
(14) |
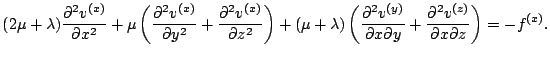 |
(15) |
Discretizing this using numerical derivatives based on finite differences (8, pp. 186-189) yields
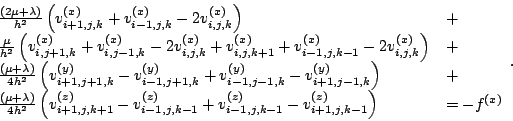 |
(16) |
With shortcuts
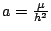 ,
,
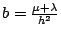 follows,
follows,
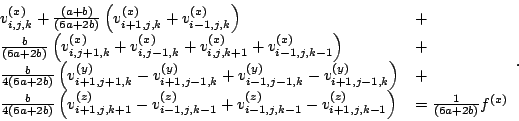 |
(17) |
y- and z- components can be obtained in a similar manner.
With
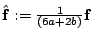 , writing (12)
in its discretized representation yields a linear system
, writing (12)
in its discretized representation yields a linear system
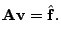 |
(18) |

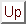

Next: SOR update
Up: Mathematical Derivations
Previous: Mathematical Derivations
Gert Wollny
2003-03-17
![]() , writing (12)
in its discretized representation yields a linear system
, writing (12)
in its discretized representation yields a linear system